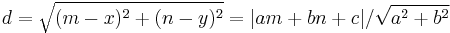Distance from a point to a line
The distance from a point to a line is the shortest distance from a point to a line in Euclidean geometry. It can be calculated in the following ways.
Contents |
Cartesian coordinates
In the case of a line in the plane given by the equation ax + by + c = 0, where a, b and c are real constants with a and b not both zero, the distance from the line to a point (x0,y0) is
Vector formulation
Suppose we express the line in vector form:
where n is a unit vector. That is, a point, x, on the line is found by moving to a point a in space, then moving t units along the direction of the line..
The distance of an arbitrary point p to this line is given by
This more general formula can be used in dimensions other than two. This equation is constructed geometrically as follows: 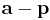 is a vector from p to the point a on the line. Then
is a vector from p to the point a on the line. Then 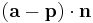 is the projected length onto the line and so
is the projected length onto the line and so
is a vector that is the projection of 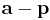 onto the line and so
onto the line and so
is the component of 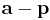 perpendicular to the line. The distance from the point to the line is then just the norm of that vector.
perpendicular to the line. The distance from the point to the line is then just the norm of that vector.
Proof 1 (algebraic proof)
Let point (x,y) be the intersection between the line ax + by + c = 0 and its perpendicular which contains (m,n), where point (m,n) is any arbitrary point on the perpendicular line to ax + by + c = 0.
Then it is necessary to show 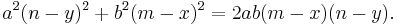
The above equation can be changed to 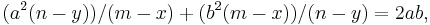 because the slope of the perpendicular to the ax+by+c which contains (x,y) and (m,n) is b/a.
because the slope of the perpendicular to the ax+by+c which contains (x,y) and (m,n) is b/a.
Then
So the distance is
Proof 2 (geometric proof)
Let the point S(m,n) connect to the point G(x,y) which is on the line ax+by+c=0, both lines being perpendicular to each other.
Draw a line am+bn+d=0, containing the point S(m,n), which is parallel to ax+by+c=0.
The absolute value of (c-d)/b, which is the distance of the line connecting the point G and some point F on the line am+bn+d=0 and parallel to the y-axis, is equal to the absolute value of (am+bn+c)/b.
Then the desired distance SG can be derived from the right triangle SGF, which is in the ratio of a:b: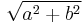 .
.
The absolute value of (am+bn+c)/b is the diagonal of the right triangle, so just multiply by the absolute value of b and divide by 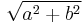 , and the proof is complete.
, and the proof is complete.
Sample code
The following Java snippet provide distance from point P to the line A-B:
public double pointToLineDistance(Point A, Point B, Point P)
{
double normalLength = Math.sqrt((B.x - A.x) * (B.x - A.x) + (B.y - A.y) * (B.y - A.y));
return Math.abs((P.x - A.x) * (B.y - A.y) - (P.y - A.y) * (B.x - A.x)) / normalLength;
}
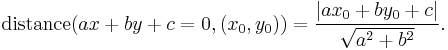
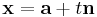
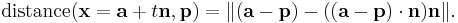
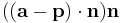
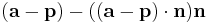
![(a^2%2Bb^2)((m-x)^2%2B(n-y)^2)=[a(m-x)%2Bb(n-y)]^2=(am%2Bbn%2Bc)^2.](/2012-wikipedia_en_all_nopic_01_2012/I/38eeac8427c0a94b58970ef24a709d1e.png)